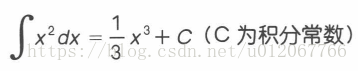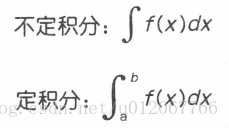專注于：

1）材料中二氧化碳的退火方法：原子vs分子

2）二氧化碳在材料中的擴(kuò)散

3）菲克定律

4）借助導(dǎo)數(shù)和積分

(1)陳的故事：材料中的二氧化碳退火方法

在致密金屬中，晶格間隙大于氫分子的直徑。 只有當(dāng)氫分子解離成氫原子時(shí)，它們才能進(jìn)入金屬并在金屬中原子擴(kuò)散。 如果晶體存在缺陷，其數(shù)量級(jí)也是千分之幾。 即只有少量氫原子在缺陷處聚合成氫分子，大部分仍以原子形式存在。

氫在微孔材料或陶瓷材料中的擴(kuò)散方式與在致密金屬中的擴(kuò)散方式不同，擴(kuò)散多項(xiàng)式與壓力之間的指數(shù)關(guān)系會(huì)發(fā)生變化。

%E8%8F%B2%E5%85%8B%E5%AE%9A%E5%BE%8B/?fr=

(2)菲克定律和物理化學(xué)方法

菲克定律包括兩個(gè)要素：

（1）早在1855年，菲克就提出，單位時(shí)間內(nèi)通過(guò)垂直于擴(kuò)散方向的單位橫截面積的擴(kuò)散物質(zhì)的通量（稱為擴(kuò)散通量flux，記為J）與含量梯度有關(guān)截面處的擴(kuò)散通量( )成反比，即含量梯度越大，擴(kuò)散通量越大。 這就是菲克第一定理。

(2)菲克第二定理是在第一定理的基礎(chǔ)上推導(dǎo)出來(lái)的。 菲克第二定理強(qiáng)調(diào)，在非穩(wěn)態(tài)擴(kuò)散過(guò)程中，在距離x處，含量隨時(shí)間的變化率等于該處擴(kuò)散通量隨距離變化率的負(fù)值。

單位時(shí)間內(nèi)，擴(kuò)散物質(zhì)通過(guò)垂直于擴(kuò)散方向的單位橫截面積的通量（稱為擴(kuò)散通量，用J表示）與橫截面處的含量梯度（ ）成反比，即含量梯度越大，擴(kuò)散通量越大。 物理表達(dá)式如下：

式中，D稱為擴(kuò)散系數(shù)（m2/s），C為擴(kuò)散物質(zhì)（成分）的體積含量（原子數(shù)/m3或kg/m3），?C/?x為含量梯度，符號(hào)“-”表示擴(kuò)散方向與含量梯度相反的方向，即擴(kuò)散成分從高含量區(qū)域向低含量區(qū)域擴(kuò)散。 擴(kuò)散通量J的單位為kg/(m2·s)

對(duì)于三維擴(kuò)散系統(tǒng)，作為矢量的擴(kuò)散通量J可以在x、y、z坐標(biāo)軸方向上分解為三個(gè)分量Jx、Jy、Jz。 此時(shí)，擴(kuò)散通量可寫為：

或者

其中，i、j、k表示x、y、z方向的單位向量。 J是擴(kuò)散通量，是三維向量場(chǎng)，D是擴(kuò)散系數(shù)，是二階張量菲克第一定律公式，C是內(nèi)容，是數(shù)場(chǎng)，▽是梯度算子。

前兩個(gè)多項(xiàng)式是菲克第一定理的物理表達(dá)式，是描述擴(kuò)散現(xiàn)象的基本多項(xiàng)式。 菲克第一定理強(qiáng)調(diào)，在任何內(nèi)容梯度驅(qū)動(dòng)的擴(kuò)散系統(tǒng)中，物質(zhì)都會(huì)沿著其內(nèi)容場(chǎng)決定的負(fù)梯度方向擴(kuò)散，擴(kuò)散流的大小與內(nèi)容梯度成反比。 值得注意的是，擴(kuò)散方程是描述宏觀擴(kuò)散現(xiàn)象的唯象關(guān)系式，不涉及擴(kuò)散系統(tǒng)內(nèi)部原子運(yùn)動(dòng)的微觀過(guò)程，而擴(kuò)散系數(shù)反映了擴(kuò)散系統(tǒng)的特性。 擴(kuò)散多項(xiàng)式中的內(nèi)容C是位置和時(shí)間的函數(shù)，擴(kuò)散系數(shù)D理論上是一個(gè)富含九個(gè)分量的二階張量，與擴(kuò)散系統(tǒng)的結(jié)構(gòu)對(duì)稱性密切相關(guān)。 [2]

擴(kuò)散介質(zhì)中擴(kuò)散物質(zhì)的含量分布隨時(shí)間變化的擴(kuò)散常稱為不穩(wěn)定擴(kuò)散，其擴(kuò)散通量隨位置和時(shí)間的變化而變化。 對(duì)于不穩(wěn)定擴(kuò)散，可以根據(jù)物質(zhì)的平衡關(guān)系構(gòu)造擴(kuò)散二階微分方程。

菲克第二定理是在第一定理的基礎(chǔ)上推導(dǎo)出來(lái)的。菲克第二定理強(qiáng)調(diào)，在非穩(wěn)態(tài)擴(kuò)散過(guò)程中，在距離x處，內(nèi)容隨時(shí)間的變化率等于內(nèi)容變化率的負(fù)值。擴(kuò)散通量隨距離的變化，以及

這就是菲克第二定理的物理表達(dá)。如果擴(kuò)散系數(shù)D隨坐標(biāo)x變化不大，可以近似看作一個(gè)常數(shù)，那么公式可以寫為

上式中，C為擴(kuò)散物質(zhì)的體積含量（kg/m^3），t為擴(kuò)散時(shí)間（s），x為距離（m）。 事實(shí)上，退火體中溶質(zhì)原子的擴(kuò)散系數(shù)D隨含量的不同而變化。 為了更容易求解擴(kuò)散多項(xiàng)式，通常將D近似視為常數(shù)。

對(duì)于各向同性三維擴(kuò)散系統(tǒng)，F(xiàn)ick 的第二擴(kuò)散多項(xiàng)式可以寫為：

對(duì)于球?qū)ΨQ擴(kuò)散，上式可以轉(zhuǎn)化為極坐標(biāo)表達(dá)式：

菲克第二擴(kuò)散多項(xiàng)式描述了在不穩(wěn)定擴(kuò)散的情況下，介質(zhì)中各點(diǎn)由于擴(kuò)散而引起的物質(zhì)含量的變化。 根據(jù)各種具體的初始條件和邊界條件，求解菲克第二擴(kuò)散多項(xiàng)式，即可得到相應(yīng)體系的物質(zhì)含量隨時(shí)間和位置變化的規(guī)律。 [2]

菲克定律中的穩(wěn)態(tài)擴(kuò)散和非穩(wěn)態(tài)擴(kuò)散

穩(wěn)態(tài)擴(kuò)散

菲克第一定理只適用于J和C不隨時(shí)間變化的場(chǎng)合——穩(wěn)態(tài)擴(kuò)散（-state）。 所謂穩(wěn)定擴(kuò)散是指擴(kuò)散過(guò)程中擴(kuò)散物質(zhì)的含量分布不隨時(shí)間變化的擴(kuò)散過(guò)程。 這類問(wèn)題可以直接用菲克第一定理解決。 對(duì)于穩(wěn)態(tài)擴(kuò)散，也可以描述為：在擴(kuò)散過(guò)程中，擴(kuò)散成分的含量C僅隨距離x變化，而不隨時(shí)間t變化。 每時(shí)刻有多少個(gè)原子從后面擴(kuò)散，向右擴(kuò)散了多少個(gè)原子，沒(méi)有盈虧，所以內(nèi)容不隨時(shí)間變化。

事實(shí)上菲克第一定律公式，大多數(shù)擴(kuò)散過(guò)程是在非穩(wěn)態(tài)條件下發(fā)生的。

非穩(wěn)態(tài)擴(kuò)散是指擴(kuò)散過(guò)程中擴(kuò)散物質(zhì)的含量分布隨時(shí)間變化的擴(kuò)散過(guò)程。 典型不穩(wěn)定擴(kuò)散中的典型邊界條件可分為兩種情況：第一種情況是擴(kuò)散過(guò)程中晶體表面擴(kuò)散粒子的含量C0保持恒定； 第二種情況是一定量的擴(kuò)散材料Q向內(nèi)擴(kuò)散。

非穩(wěn)態(tài)擴(kuò)散（-態(tài)）的特點(diǎn)是擴(kuò)散過(guò)程中J隨時(shí)間和距離的變化而變化。 經(jīng)過(guò)各處的擴(kuò)散通量J隨距離x而變化，而穩(wěn)態(tài)擴(kuò)散的擴(kuò)散通量處處相等，不隨時(shí)間變化。 對(duì)于非穩(wěn)態(tài)擴(kuò)散，需要應(yīng)用菲克第二定理。 [2]

(3)微積分的補(bǔ)充知識(shí)：

導(dǎo)數(shù)基本公式

1/x 的行列式是 -1/x^2。

(u/v)'=(u'*vu*v')/(v^bai2) 可用，

(1/x)'=(1'*x-1*x')/x^2=-1/x^2

x 的 n 次方行列式

函數(shù)積 (f(x)*g(x)) 導(dǎo)數(shù)

積分常數(shù)

現(xiàn)有的雙面表達(dá)式：

這意味著“找到 x

關(guān)于x的積分”。積分是行列式的逆運(yùn)算，所以可以換個(gè)思路：“關(guān)于x，導(dǎo)數(shù)得到

"的函數(shù)是什么，得到的函數(shù)就是上面表達(dá)式的積分，即：函數(shù)

導(dǎo)數(shù)的結(jié)果是

向上。 但顯然這不是正確的答案。 由于常數(shù)項(xiàng)在導(dǎo)數(shù)之后將被消除，因此，

的積分（主函數(shù)）有無(wú)限多個(gè)表示形式 (

+2,

+11 等）。 因此，此時(shí)應(yīng)該這樣處理：

使用字母C表示所有可以用作常數(shù)項(xiàng)的數(shù)字。

原始

對(duì) f(x) 進(jìn)行不定積分得到的函數(shù)稱為原函數(shù)。原函數(shù)可寫為

，也可以用小寫的f表示：F(x)。

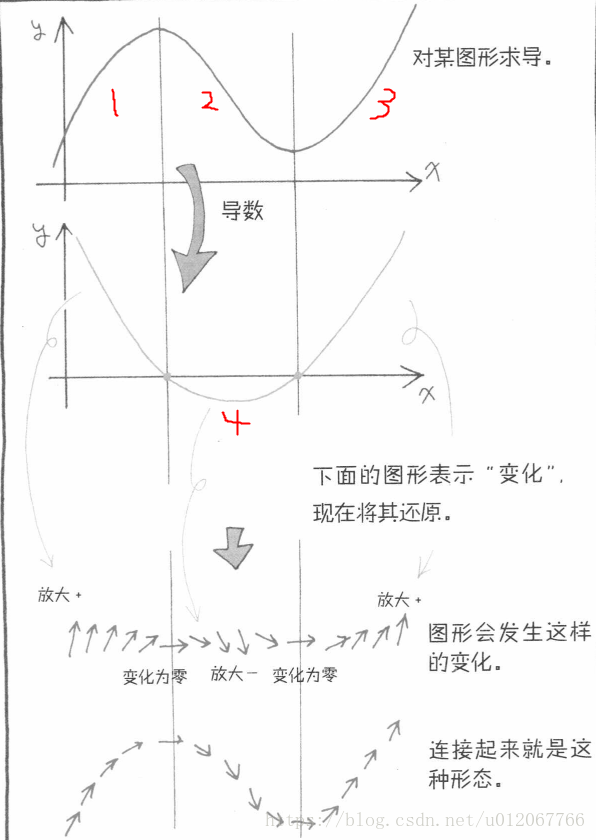
圖的導(dǎo)數(shù)

在前面的反例中，為什么“2”部分原函數(shù)的行列式圖像看起來(lái)像“4”？ 這是因?yàn)榇藭r(shí)“2”部分對(duì)應(yīng)的函數(shù)的斜率（行列式）為負(fù)值。 根據(jù)曲線的變化，不難看出斜率先減小后減小，因此對(duì)應(yīng)的行列式圖像為“4”。 看。

如果行列式代表變化的情況，那么積分就代表變化的集合。

與區(qū)間范圍積分

定積分是一個(gè)區(qū)間上的積分：

定積分的積分?jǐn)?shù)上下都有字母，表示“從哪里到哪里的范圍”，“從哪里”在下面，“到哪里”在上面，所以

范圍是從a到b。

到了該努力工作的年紀(jì)，找份穩(wěn)定的工作，然后你就會(huì)發(fā)現(xiàn)，自己窮也安定了。

貧窮限制了我們的想象力，而我們的想象力不能被貧窮阻止。 現(xiàn)在就開(kāi)始努力吧，也許你就能拼出大器晚成。

%E5%AF%BC%E6%95%B0

這里列出了 14 個(gè)基本初等函數(shù)的導(dǎo)數(shù)。

函數(shù) 原函數(shù) 導(dǎo)函數(shù)

常數(shù)函數(shù)

（即常數(shù)）

（C為常數(shù)）

指數(shù)函數(shù)

電源功能

對(duì)數(shù)函數(shù)

余弦函數(shù)

正弦函數(shù)

余弦函數(shù)

余切函數(shù)

割函數(shù)

余割函數(shù)

反余弦函數(shù)

反正弦函數(shù)

簡(jiǎn)而言之，正切函數(shù)

反余切函數(shù)

雙曲函數(shù)

復(fù)雜函數(shù)

1、導(dǎo)數(shù)的四種算術(shù)運(yùn)算：

高階行列式算法

……………….①

………………②

………………③

2、原函數(shù)的行列式與反函數(shù)的關(guān)系（從三角函數(shù)的行列式推導(dǎo)出反三角函數(shù)）：

y=f(x) 的反函數(shù)為 x=g(y)，則 y'=1/x'。

3、復(fù)合函數(shù)的推導(dǎo)：

復(fù)合函數(shù)對(duì)自變量的行列式等于已知函數(shù)對(duì)中間變量的行列式除以中間變量對(duì)自變量的行列式（稱為鏈?zhǔn)椒▌t）。

4、變極限積分的求導(dǎo)規(guī)則：

（a(x)、b(x) 是子函數(shù)）

行列式的估計(jì)

估計(jì)已知函數(shù)的導(dǎo)數(shù)可以根據(jù)行列式的定義，利用變化率的極限來(lái)估計(jì)。 在實(shí)際估計(jì)中，大多數(shù)常見(jiàn)的解析函數(shù)都可以看作是一些簡(jiǎn)單函數(shù)的和、差、積、商或復(fù)合結(jié)果。 只要知道這個(gè)簡(jiǎn)單函數(shù)的導(dǎo)函數(shù)，就可以根據(jù)行列式的導(dǎo)數(shù)規(guī)則來(lái)估計(jì)更復(fù)雜函數(shù)的導(dǎo)函數(shù)。

行列式的導(dǎo)數(shù)定律

由基本函數(shù)的和、差、積、商或互復(fù)合組成的函數(shù)的導(dǎo)函數(shù)，可以通過(guò)函數(shù)的導(dǎo)數(shù)規(guī)則推導(dǎo)出來(lái)。 基本衍生規(guī)則如下：

1、求導(dǎo)的線性性：函數(shù)線性組合的導(dǎo)數(shù)等于先對(duì)它們各自求偏導(dǎo)數(shù)，然后再取線性組合（即公式①）。

2、兩個(gè)函數(shù)乘積的導(dǎo)函數(shù)：一導(dǎo)數(shù)乘二+一乘二導(dǎo)數(shù)（即公式②）。

3、兩個(gè)函數(shù)商的導(dǎo)數(shù)函數(shù)也是一個(gè)多項(xiàng)式：（子導(dǎo)數(shù)乘以母-子導(dǎo)數(shù)乘以母導(dǎo)數(shù)）乘以母平方（即公式③）。

4. 如果存在復(fù)合函數(shù)，則使用鏈?zhǔn)椒▌t導(dǎo)數(shù)。

高階導(dǎo)數(shù)

如何找到高階行列式

1、直接法：從高階行列式的定義中逐步求出高階行列式。

通常用于尋找解決問(wèn)題的能力。

2、高階行列式算法：

（牛頓-萊布尼茲公式）

3、間接法：借助已知的高階行列式公式，通過(guò)四次算術(shù)運(yùn)算、變量代換等。

注意：代入后，函數(shù)應(yīng)該很容易求出，盡量接近已知公式來(lái)求階行列式。

公式

為了方便記憶，有人整理了如下公式：

上一篇： VASP 錯(cuò)誤: :error(78):()

下一篇： 菲克定律：材料中二氧化碳分子的退火和隨后的擴(kuò)散